Paged Attention¶

警告

這是一份基於 vLLM 原始論文的歷史文件。它不再描述 vLLM 目前的程式碼。

目前，vLLM 使用其自實現的**多頭查詢注意力核函式** (csrc/attention/attention_kernels.cu)。此核函式旨在與 vLLM 的分頁 KV 快取相容，其中鍵和值快取儲存在單獨的塊中（請注意，此塊概念不同於 GPU 執行緒塊。因此，在後續文件中，我將 vLLM 分頁注意力塊稱為“塊”，而將 GPU 執行緒塊稱為“執行緒塊”）。

為了實現高效能，此核函式依賴於特別設計的記憶體佈局和訪問方法，特別是線上程將資料從全域性記憶體讀取到共享記憶體時。本文件旨在逐步提供對核函式實現的**高層解釋**，以幫助那些希望瞭解 vLLM 多頭查詢注意力核函式的人。閱讀本文件後，使用者將可能更好地理解並更容易遵循實際實現。

請注意，本文件可能不會涵蓋所有細節，例如如何計算相應資料的正確索引或點積實現。然而，在閱讀本文件並熟悉高層邏輯流程後，您應該更容易閱讀實際程式碼並理解細節。

輸入¶

核函式接收一個引數列表，供當前執行緒執行其分配的任務。最重要的三個引數是輸入指標 q、k_cache 和 v_cache，它們指向全域性記憶體中需要讀取和處理的查詢、鍵和值資料。輸出指標 out 指向結果應寫入的全域性記憶體。這四個指標實際上指向多維陣列，但每個執行緒僅訪問分配給它的資料部分。為簡化起見，我已省略了所有其他執行時引數。

template<typename scalar_t, int HEAD_SIZE, int BLOCK_SIZE, int NUM_THREADS, int PARTITION_SIZE = 0>
__device__ void paged_attention_kernel(
    ... // Other side args.
    const scalar_t* __restrict__ out,       // [num_seqs, num_heads, max_num_partitions, head_size]
    const scalar_t* __restrict__ q,         // [num_seqs, num_heads, head_size]
    const scalar_t* __restrict__ k_cache,   // [num_blocks, num_kv_heads, head_size/x, block_size, x]
    const scalar_t* __restrict__ v_cache,   // [num_blocks, num_kv_heads, head_size, block_size]
    ... // Other side args.
)

函式簽名上方還有一組在編譯時確定的模板引數。scalar_t 表示查詢、鍵和值資料元素的**資料型別**，例如 FP16。HEAD_SIZE 表示每個頭的元素數量。BLOCK_SIZE 表示每個塊中的**token 數量**。NUM_THREADS 表示每個執行緒塊中的執行緒數量。PARTITION_SIZE 表示張量並行 GPU 的數量（為簡單起見，我們假設此值為 0，並且張量並行已停用）。

有了這些引數，我們需要進行一系列準備工作。這包括計算當前頭的索引、塊索引和其他必要的變數。不過，目前我們可以忽略這些準備工作，直接進行實際計算。一旦我們掌握了整個流程，理解它們會更容易。

概念¶

在深入計算流程之前，我想描述幾個後續部分需要用到的概念。不過，如果您遇到任何令人困惑的術語，可以跳過此部分，稍後返回。

序列 (Sequence)：序列代表一個客戶端請求。例如，q 指向的資料形狀為 [num_seqs, num_heads, head_size]。這表示 q 指向的總共有 num_seqs 個查詢序列資料。由於此核函式是單個查詢注意力核函式，每個序列只有一個查詢 token。因此，num_seqs 等於批處理中處理的總 token 數。
上下文 (Context)：上下文由序列生成的 token 組成。例如，["What", "is", "your"] 是上下文 token，輸入查詢 token 是 "name"。模型可能會生成 token "?"。
向量 (Vec)：向量是**一起獲取和計算的元素列表**。對於查詢和鍵資料，向量大小 (VEC_SIZE) 的確定方式是使每個執行緒組一次可以獲取和計算 16 位元組的資料。對於值資料，向量大小 (V_VEC_SIZE) 的確定方式是使每個執行緒一次可以獲取和計算 16 位元組的資料。例如，如果 scalar_t 是 FP16（2 位元組）且 THREAD_GROUP_SIZE 為 2，則 VEC_SIZE 將為 4，而 V_VEC_SIZE 將為 8。
執行緒組 (Thread group)：執行緒組是**一次獲取和計算一個查詢 token 和一個鍵 token 的小執行緒組** (THREAD_GROUP_SIZE)。每個執行緒只處理 token 資料的一部分。一個執行緒組處理的總元素數量稱為 x。例如，如果執行緒組包含 2 個執行緒且頭大小為 8，則執行緒 0 處理索引為 0、2、4、6 的查詢和鍵元素，而執行緒 1 處理索引為 1、3、5、7 的元素。
塊 (Block)：vLLM 中的鍵和值快取資料被**分成塊**。每個塊儲存一個頭的固定數量（BLOCK_SIZE）的 token 的資料。每個塊可能只包含整個上下文 token 的一部分。例如，如果塊大小為 16 且頭大小為 128，則對於一個頭，一個塊可以儲存 16 * 128 = 2048 個元素。
Warp (執行緒束)：Warp 是**32 個執行緒的組** (WARP_SIZE)，它們在流多處理器 (SM) 上同時執行。在此核函式中，每個 warp 一次處理一個查詢 token 與一個**整個塊**的鍵 token 之間的計算（它可能在多次迭代中處理多個塊）。例如，如果一個上下文有 4 個 warp 和 6 個塊，則分配方式如下：warp 0 處理第 0、4 個塊，warp 1 處理第 1、5 個塊，warp 2 處理第 2 個塊，warp 3 處理第 3 個塊。
執行緒塊 (Thread block)：執行緒塊是**一組執行緒** (NUM_THREADS)，它們可以訪問相同的共享記憶體。每個執行緒塊包含多個 warp（NUM_WARPS），在此核函式中，每個執行緒塊處理一個查詢 token 與**整個上下文**的鍵 token 之間的計算。
網格 (Grid)：網格是執行緒塊的集合，並定義了該集合的形狀。在此核函式中，形狀為 (num_heads, num_seqs, max_num_partitions)。因此，每個執行緒塊只處理一個頭、一個序列和一個分割槽的計算。

查詢¶

本節將介紹查詢資料在記憶體中的儲存方式以及每個執行緒如何獲取它。如上所述，每個執行緒組獲取一個查詢 token 資料，而每個執行緒本身只處理一個查詢 token 資料的一部分。在每個 warp 中，每個執行緒組將獲取相同的查詢 token 資料，但會將其與不同的鍵 token 資料相乘。

const scalar_t* q_ptr = q + seq_idx * q_stride + head_idx * HEAD_SIZE;

每個執行緒定義自己的 q_ptr，它指向全域性記憶體中分配的查詢 token 資料。例如，如果 VEC_SIZE 為 4 且 HEAD_SIZE 為 128，則 q_ptr 指向的資料包含總共 128 個元素，分為 128 / 4 = 32 個向量。

__shared__ Q_vec q_vecs[THREAD_GROUP_SIZE][NUM_VECS_PER_THREAD];

接下來，我們需要將 q_ptr 指向的全域性記憶體資料讀取到共享記憶體中，作為 q_vecs。需要注意的是，每個向量被分配到不同的行。例如，如果 THREAD_GROUP_SIZE 為 2，執行緒 0 將處理第 0 行向量，而執行緒 1 處理第 1 行向量。透過以這種方式讀取查詢資料，相鄰的執行緒（如執行緒 0 和執行緒 1）可以讀取相鄰的記憶體，實現記憶體合併以提高效能。

鍵¶

與“查詢”部分類似，本節介紹鍵的記憶體佈局和分配。雖然每個執行緒組在一個核函式執行中只處理一個查詢 token，但它可能在多次迭代中處理多個鍵 token。同時，每個 warp 將在多次迭代中處理多個塊的鍵 token，以確保在核函式執行後，所有上下文 token 都被整個執行緒組處理。在此上下文中，“處理”是指執行查詢資料和鍵資料之間的點積運算。

const scalar_t* k_ptr = k_cache + physical_block_number * kv_block_stride
                    + kv_head_idx * kv_head_stride
                    + physical_block_offset * x;

與 q_ptr 不同，每個執行緒中的 k_ptr 在不同的迭代中指向不同的鍵 token。如上所示，k_ptr 指向基於已分配的塊、已分配的頭和已分配的 token 的鍵 token 資料。

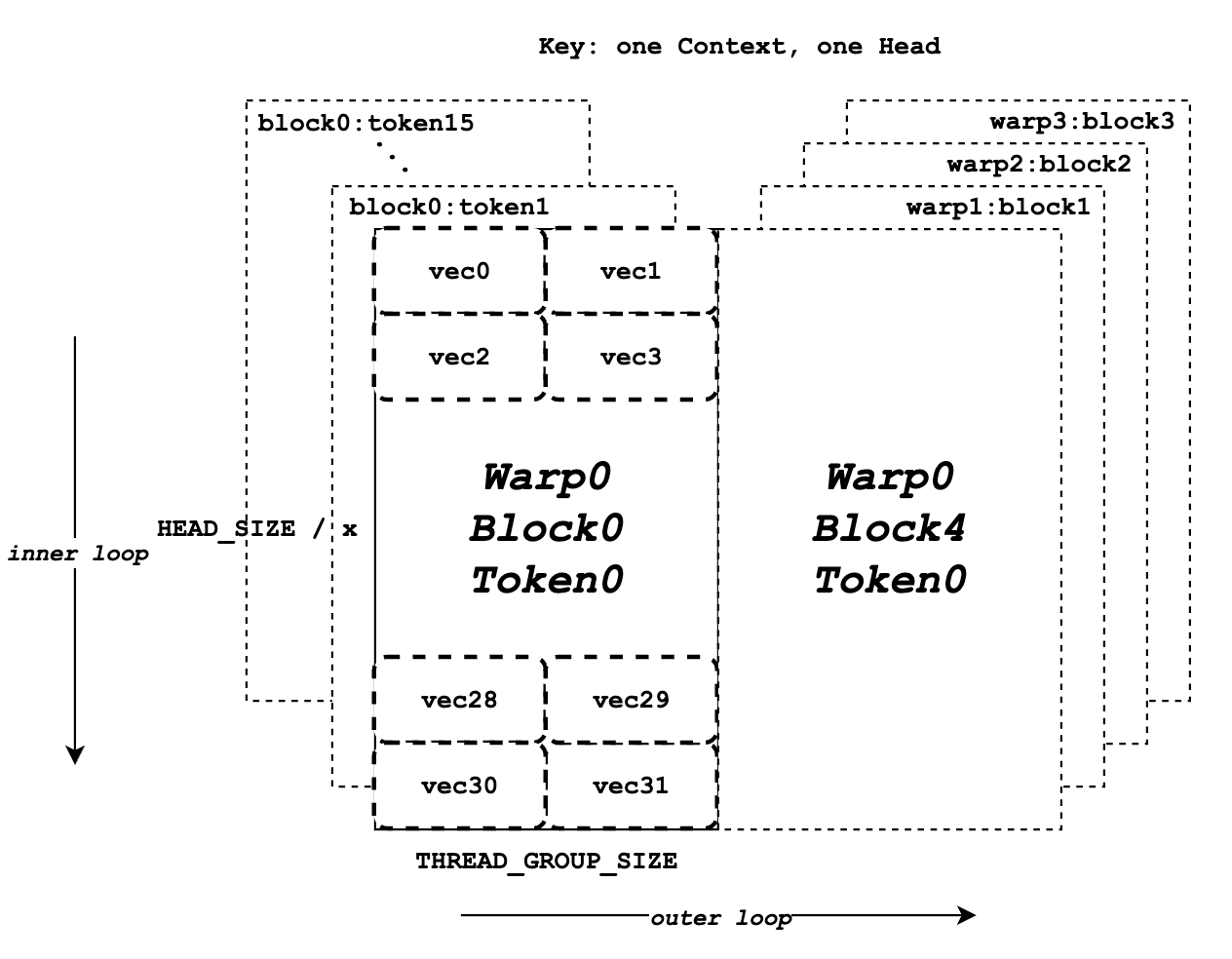
上圖說明了鍵資料的記憶體佈局。它假設 BLOCK_SIZE 為 16，HEAD_SIZE 為 128，x 為 8，THREAD_GROUP_SIZE 為 2，並且總共有 4 個 warp。每個矩形代表一個頭上的一個鍵 token 的所有元素，它將由一個執行緒組處理。左半部分顯示了 warp 0 的總共 16 個塊的鍵 token 資料，而右半部分代表其他 warp 或迭代的剩餘鍵 token 資料。在每個矩形內部，總共有 32 個向量（一個 token 的 128 個元素）將由 2 個執行緒（一個執行緒組）單獨處理。

K_vec k_vecs[NUM_VECS_PER_THREAD]

接下來，我們需要將鍵 token 資料從 k_ptr 讀取並存儲到暫存器記憶體中，作為 k_vecs。我們使用暫存器記憶體來儲存 k_vecs，因為 k_vecs 只會被一個執行緒訪問一次，而 q_vecs 會被多個執行緒多次訪問。每個 k_vecs 將包含多個向量用於後續計算。每個向量將在每次內部迭代中設定。向量的分配允許 warp 中的相鄰執行緒一起讀取相鄰記憶體，再次促進記憶體合併。例如，執行緒 0 將讀取向量 0，而執行緒 1 將讀取向量 1。在下一次內部迴圈中，執行緒 0 將讀取向量 2，而執行緒 1 將讀取向量 3，依此類推。

您可能對整體流程仍然有些困惑。不用擔心，請繼續閱讀下一節“QK”。它將以更清晰、更高階的方式說明查詢和鍵的計算流程。

QK¶

如下面的虛擬碼所示，在整個 for 迴圈塊之前，我們獲取一個 token 的查詢資料並將其儲存在 q_vecs 中。然後，在外層 for 迴圈中，我們迭代不同的 k_ptrs（指向不同的 token），並在內層 for 迴圈中準備 k_vecs。最後，我們執行 q_vecs 和每個 k_vecs 之間的點積運算。

q_vecs = ...
for ... {
    k_ptr = ...
    for ... {
        k_vecs[i] = ...
    }
    ...
    float qk = scale * Qk_dot<scalar_t, THREAD_GROUP_SIZE>::dot(q_vecs[thread_group_offset], k_vecs);
}

如前所述，對於每個執行緒，它一次只獲取一部分查詢和鍵 token 資料。然而，在 Qk_dot<>::dot 中會發生跨執行緒組的規約。因此，這裡返回的 qk 不僅僅是查詢和鍵部分 token 的點積運算結果，而是實際上是整個查詢和鍵 token 資料的完整結果。

例如，如果 HEAD_SIZE 的值為 128 且 THREAD_GROUP_SIZE 為 2，每個執行緒的 k_vecs 將包含總共 64 個元素。然而，返回的 qk 實際上是 128 個查詢元素和 128 個鍵元素之間點積運算的結果。如果您想了解有關點積和規約實現的更多詳細資訊，可以參考 Qk_dot<>::dot 的實現。但為了簡化起見，本文件不作介紹。

Softmax¶

接下來，我們需要計算所有 qk 的歸一化 softmax，如上所示，其中每個 \(x\) 代表一個 qk。為此，我們必須獲得所有 qk 的 qk_max（\(m(x)\)）的規約值和 exp_sum（\(\ell(x)\)）。規約應在整個執行緒塊上執行，包括查詢 token 與所有上下文鍵 token 之間的結果。

\[ \begin{gather*} m(x):=\max _i \quad x_i \\ \quad f(x):=\left[\begin{array}{lll}e^{x_1-m(x)} & \ldots & e^{x_B-m(x)}\end{array}\right]\\ \quad \ell(x):=\sum_i f(x)_i \\ \quad \operatorname{softmax}(x):=\frac{f(x)}{\ell(x)} \end{gather*} \]

`qk_max` 和 `logits`¶

在我們獲得 qk 結果後，我們就可以用 qk 設定臨時的 logits 結果（最終 logits 應該儲存歸一化 softmax 結果）。同時，我們可以比較並收集當前執行緒組計算的所有 qk 的 qk_max。

if (thread_group_offset == 0) {
    const bool mask = token_idx >= context_len;
    logits[token_idx - start_token_idx] = mask ? 0.f : qk;
    qk_max = mask ? qk_max : fmaxf(qk_max, qk);
}

請注意，這裡的 logits 位於共享記憶體中，因此每個執行緒組將設定其自身分配的上下文 token 的欄位。總的來說，logits 的大小應該是上下文 token 的數量。

for (int mask = WARP_SIZE / 2; mask >= THREAD_GROUP_SIZE; mask /= 2) {
    qk_max = fmaxf(qk_max, VLLM_SHFL_XOR_SYNC(qk_max, mask));
}

if (lane == 0) {
    red_smem[warp_idx] = qk_max;
}

然後，我們需要獲取每個 warp 上的規約 qk_max。主要思想是讓 warp 中的執行緒相互通訊並獲得最終的最大 qk。

for (int mask = NUM_WARPS / 2; mask >= 1; mask /= 2) {
    qk_max = fmaxf(qk_max, VLLM_SHFL_XOR_SYNC(qk_max, mask));
}
qk_max = VLLM_SHFL_SYNC(qk_max, 0);

最後，我們可以透過比較此執行緒塊中所有 warp 的 qk_max 來獲得整個執行緒塊的規約 qk_max。然後，我們需要將最終結果廣播到每個執行緒。

`exp_sum`¶

與 qk_max 類似，我們也需要從整個執行緒塊中獲取規約和值。

for (int i = thread_idx; i < num_tokens; i += NUM_THREADS) {
    float val = __expf(logits[i] - qk_max);
    logits[i] = val;
    exp_sum += val;
}
...
exp_sum = block_sum<NUM_WARPS>(&red_smem[NUM_WARPS], exp_sum);

首先，將每個執行緒組的所有 exp 值相加，同時將 logits 中的每個條目從 qk 轉換為 exp(qk - qk_max)。請注意，這裡的 qk_max 已經是整個執行緒塊中的最大 qk。然後，我們可以像 qk_max 一樣對整個執行緒塊進行 exp_sum 的規約。

const float inv_sum = __fdividef(1.f, exp_sum + 1e-6f);
for (int i = thread_idx; i < num_tokens; i += NUM_THREADS) {
    logits[i] *= inv_sum;
}

最後，有了規約後的 qk_max 和 exp_sum，我們可以得到最終的歸一化 softmax 結果作為 logits。這個 logits 變數將在後續步驟中用於與值資料進行點積運算。現在，它應該儲存所有已分配上下文 token 的 qk 的歸一化 softmax 結果。

值¶

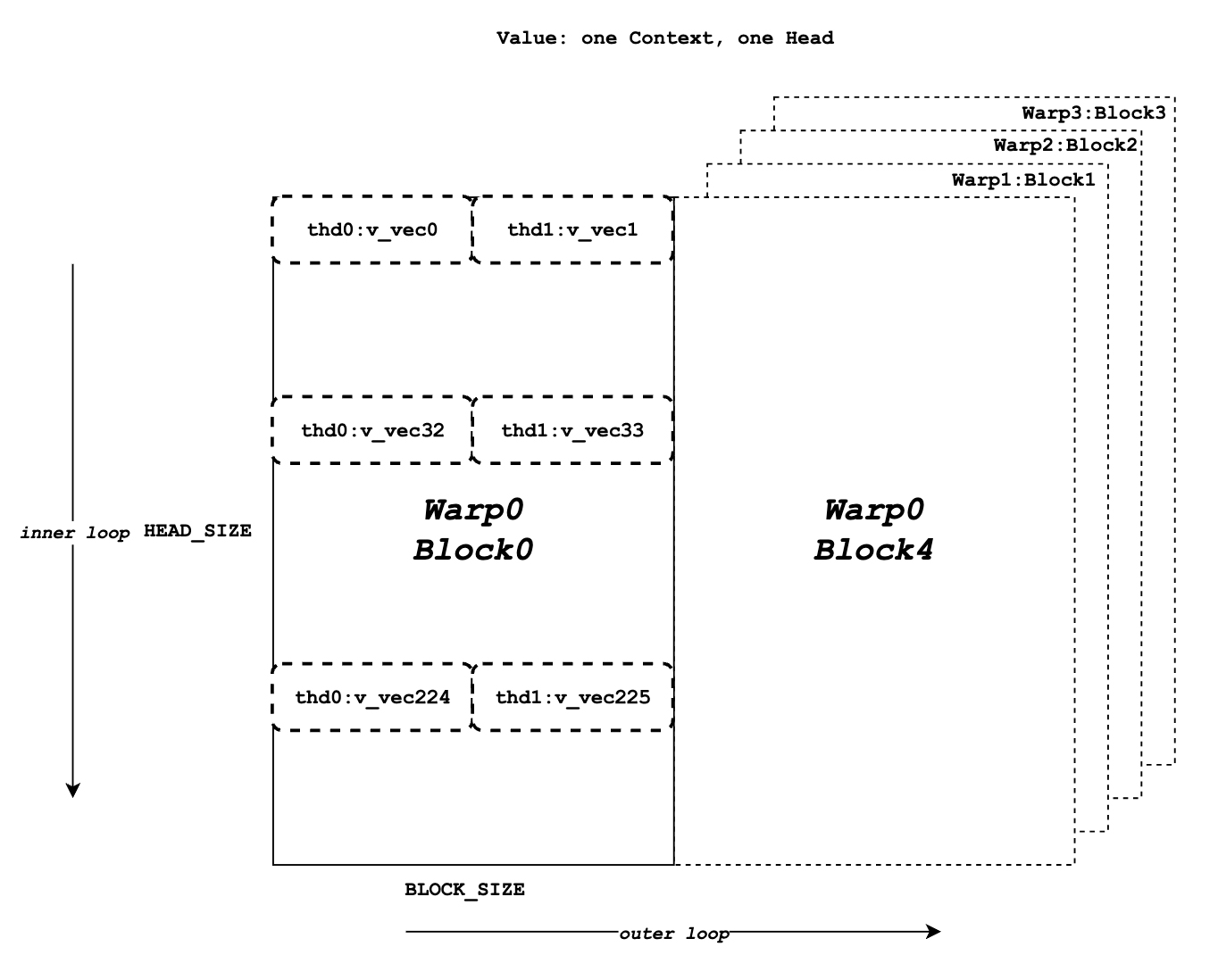
現在我們需要檢索值資料並與 logits 進行點積運算。與查詢和鍵不同，值資料沒有執行緒組的概念。如圖所示，與鍵 token 的記憶體佈局不同，同一列中的元素對應於同一個值 token。對於一個塊的值資料，有 HEAD_SIZE 行和 BLOCK_SIZE 列，它們被分成多個 v_vecs。

每個執行緒一次總是從相同數量 (V_VEC_SIZE) 的 token 中獲取 V_VEC_SIZE 個元素。結果是，單個執行緒透過多次內部迭代從不同的行和相同的列檢索多個 v_vec。對於每個 v_vec，它需要與對應的 logits_vec（也是 V_VEC_SIZE 個元素）進行點積運算。總的來說，透過多次內部迭代，每個 warp 將處理一個塊的值 token。透過多次外部迭代，整個上下文值 token 都被處理。

float accs[NUM_ROWS_PER_THREAD];
for ... { // Iteration over different blocks.
    logits_vec = ...
    for ... { // Iteration over different rows.
        v_vec = ...
        ...
        accs[i] += dot(logits_vec, v_vec);
    }
}

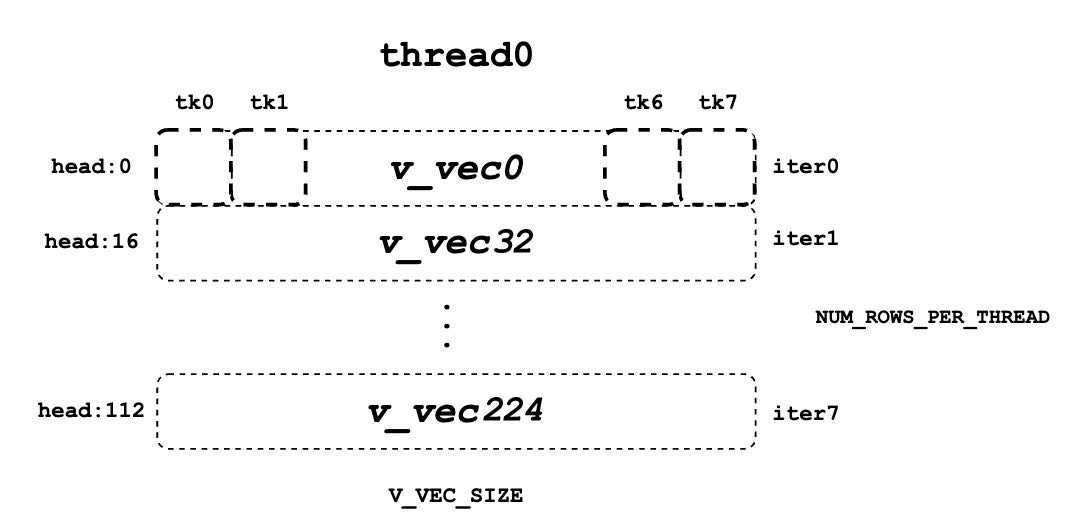
如上所示的虛擬碼，在外層迴圈中，與 k_ptr 類似，logits_vec 迭代不同的塊並從 logits 中讀取 V_VEC_SIZE 個元素。在內層迴圈中，每個執行緒從相同的 token 中讀取 V_VEC_SIZE 個元素作為 v_vec 並執行點積運算。需要注意的是，在每次內層迭代中，執行緒為相同的 token 獲取不同的頭位置元素。點積結果然後累積在 accs 中。因此，accs 的每個條目都對映到當前執行緒分配的頭位置。

例如，如果 BLOCK_SIZE 為 16 且 V_VEC_SIZE 為 8，每個執行緒一次會獲取 8 個 token 的 8 個值元素。每個元素來自相同頭位置的不同 token。如果 HEAD_SIZE 為 128 且 WARP_SIZE 為 32，對於每個內部迴圈，一個 warp 需要獲取 WARP_SIZE * V_VEC_SIZE = 256 個元素。這意味著一個 warp 處理一個塊的值 token 需要總共 128 * 16 / 256 = 8 次內部迭代。並且每個執行緒中的每個 accs 包含 8 個元素，這些元素是在 8 個已分配的 token 上累積的。對於執行緒 0，accs 變數將有 8 個元素，它們是來自所有已分配的 8 個 token 累積的值頭的第 0、32 ... 224 個元素。

LV¶

現在，我們需要在每個 warp 內執行 accs 的規約。這個過程允許每個執行緒累積一個塊中所有 token 的已分配頭位置的 accs。

for (int i = 0; i < NUM_ROWS_PER_THREAD; i++) {
    float acc = accs[i];
    for (int mask = NUM_V_VECS_PER_ROW / 2; mask >= 1; mask /= 2) {
        acc += VLLM_SHFL_XOR_SYNC(acc, mask);
    }
    accs[i] = acc;
}

接下來，我們執行所有 warp 之間的 accs 規約，允許每個執行緒獲得所有上下文 token 的已分配頭位置的 accs 累積值。請注意，每個執行緒中的每個 accs 只儲存整個頭中所有上下文 token 元素的一部分累積值。然而，總的來說，輸出的所有結果都已計算完畢，只是儲存在不同的執行緒暫存器記憶體中。

程式碼

float* out_smem = reinterpret_cast<float*>(shared_mem);
for (int i = NUM_WARPS; i > 1; i /= 2) {
    // Upper warps write to shared memory.
    ...
    float* dst = &out_smem[(warp_idx - mid) * HEAD_SIZE];
    for (int i = 0; i < NUM_ROWS_PER_THREAD; i++) {
        ...
        dst[row_idx] = accs[i];
    }

    // Lower warps update the output.
    const float* src = &out_smem[warp_idx * HEAD_SIZE];
    for (int i = 0; i < NUM_ROWS_PER_THREAD; i++) {
        ...
        accs[i] += src[row_idx];
    }

    // Write out the accs.
}

輸出¶

現在我們可以將所有計算結果從本地暫存器記憶體寫入最終輸出的全域性記憶體。

scalar_t* out_ptr = out + seq_idx * num_heads * max_num_partitions * HEAD_SIZE
                + head_idx * max_num_partitions * HEAD_SIZE
                + partition_idx * HEAD_SIZE;

首先，我們需要定義 out_ptr 變數，它指向已分配序列和已分配頭的起始地址。

for (int i = 0; i < NUM_ROWS_PER_THREAD; i++) {
    const int row_idx = lane / NUM_V_VECS_PER_ROW + i * NUM_ROWS_PER_ITER;
    if (row_idx < HEAD_SIZE && lane % NUM_V_VECS_PER_ROW == 0) {
        from_float(*(out_ptr + row_idx), accs[i]);
    }
}

最後，我們需要迭代不同的已分配頭位置，並根據 out_ptr 寫入相應的累積結果。

引用¶

@inproceedings{kwon2023efficient,
  title={Efficient Memory Management for Large Language Model Serving with PagedAttention},
  author={Woosuk Kwon and Zhuohan Li and Siyuan Zhuang and Ying Sheng and Lianmin Zheng and Cody Hao Yu and Joseph E. Gonzalez and Hao Zhang and Ion Stoica},
  booktitle={Proceedings of the ACM SIGOPS 29th Symposium on Operating Systems Principles},
  year={2023}
}

Paged Attention¶

輸入¶

概念¶

查詢¶

鍵¶

QK¶

Softmax¶

qk_max 和 logits¶

exp_sum¶

值¶

LV¶

輸出¶

引用¶

`qk_max` 和 `logits`¶

`exp_sum`¶